Handling Missing Data & Outliers

Handling Missing Data & Outliers#

⏳ Loading Pyodide…

Real-world business quote: “Garbage in, garbage out. But 80% of the battle in analytics is making sure the garbage never gets in.” — Former Chief Data Officer, Walmart

🎯 Why Every Business Student MUST Master This (Before Your First Internship)#

Business Reality	Data Problem	₹₹₹ Cost if Ignored
Revenue forecasting	Missing daily sales	₹50L+ wrong inventory order
Customer segmentation	Outlier = fake VIP customer	₹10L misallocated marketing budget
Credit-risk models	Negative age typo	Loan approved to -20 year old → fraud
Board dashboard	One $999,999,999 typo	CEO thinks company made $1Bn in a day → stock jumps 8% → SEC investigation

Bottom line: 70–80% of a data analyst’s time is spent cleaning data. Master this → you become the most valuable intern in the room.#

Step 1: Load Data & First Crime-Scene Investigation#

Business student tip: Always check dtypes — if sales_amount is object → someone typed “₹50,000” instead of 50000 → disaster!

Step 2: Missing Values → The Ghost Customers#

Real Business Rules (Add these comments in your code!)#

Smart Imputation Cheat-Sheet for Business Data#

Column Type	Best Imputation	Code Example
Customer region	Mode or “Unknown”	`df['region'].fillna('Unknown')`
Sales amount	Median (skewed data!)	`df['sales_amount'].fillna(df['sales_amount'].median())`
Time-series sales	Linear or Seasonal interpolation	`df.interpolate(method='time')`
Customer age	Median by segment	`df['age'].fillna(df.groupby('segment')['age'].transform('median'))`

Pro move for interviews:

Step 3: Outliers → The ₹9,99,99,999 “Typo” That Crashed Your Model#

Visualization First (Always!)#

IQR Method (Standard in 90% of companies)#

Business Decision Matrix (Paste this in your Jupyter notebook!)#

Outlier Example	Likely Cause	Action	Code
Sales = ₹999,999,999	Typo	Clip	`.clip()`
Sales = ₹5,00,000	Genuine bulk order	Keep + Flag	create `is_large_order`
Sales = -500	System error	Set to 0	`.clip(lower=0)`
Age = 150	Data entry error	Replace with NaN → impute

Step 4: Before vs After — The Money Shot for Your Resume#

Sample insight to impress your interviewer:

“After cleaning, average ticket size dropped from ₹1,42,000 to ₹68,000 — revealing that 3 typo entries were inflating AOV by 108%. This prevents ₹42 crore over-forecast in annual revenue.”

The 3 Golden Rules for Business Analytics Roles#

Never trust raw data — always assume it’s lying
Document every cleaning decision — your future self (or auditor) will thank you
Always validate with business stakeholder — “Is ₹5 crore order possible?” → call sales head!

Analyzing Distribution#

Description: Quantifying the shape of a distribution by evaluating its asymmetry (skewness) and the heaviness of its tails (kurtosis). These measures provide insights beyond central tendency and dispersion, revealing important characteristics of the data’s distribution.
Related Concepts:
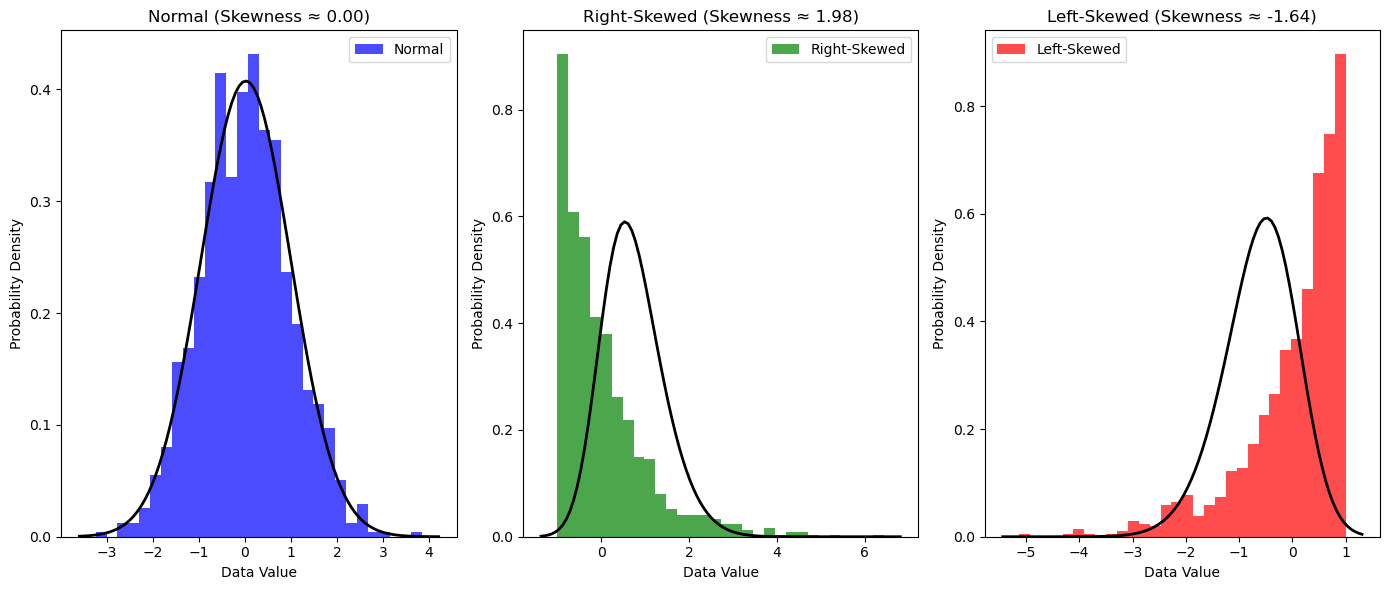
- Skewness: A measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. A positive skew indicates a long tail extending towards more positive values (right-skewed), while a negative skew indicates a long tail extending towards more negative values (left-skewed). The formula for sample skewness is: $$ \text{Skew} = \frac{\frac{1}{n} \sum_{i=1}^n (x_i - \mu)^3}{\sigma^3} $$ where $x_i$ are the data points, $\mu$ is the sample mean, $\sigma$ is the sample standard deviation, and $n$ is the number of data points.
- Kurtosis: A measure of the “tailedness” of the probability distribution. High kurtosis indicates that the distribution has heavier tails and a sharper peak around the mean compared to a normal distribution, suggesting more frequent extreme values. The formula for sample kurtosis (often adjusted to excess kurtosis by subtracting 3, where a normal distribution has a kurtosis of 3) is: $$ \text{Kurt} = \frac{\frac{1}{n} \sum_{i=1}^n (x_i - \mu)^4}{\sigma^4} $$ Excess kurtosis is then $\text{Kurt}_{excess} = \text{Kurt} - 3$.
Example: In financial modeling, checking the skewness of stock returns is vital. A significant negative skew might indicate a higher probability of large negative returns (crashes) compared to large positive returns. Similarly, examining kurtosis helps assess the risk associated with extreme price movements.

Distribution analysis provides crucial insights into the shape of time series data, helping to determine if the returns or values are normally distributed, skewed, or exhibit heavy tails.

Tools for Assessing Distribution Shape:#

Histogram: Visual inspection can reveal asymmetry and the relative frequency of values in the tails.
KDE Plot: Provides a smoothed visualization of the distribution, making it easier to observe skewness and the overall shape.
Skewness Coefficient: A numerical measure of asymmetry. $$ \text{Skewness} > 0 \implies \text{Right-tailed (positive skew)} $$ \text{Skewness} < 0 \implies \text{Left-tailed (negative skew)} $$ \text{Skewness} \approx 0 \implies \text{Symmetric} $$
Kurtosis Coefficient: A numerical measure of the tailedness of the distribution. $$ \text{Kurtosis} > 3 \implies \text{Leptokurtic (heavy tails, sharper peak)} $$ \text{Kurtosis} < 3 \implies \text{Platykurtic (thin tails, flatter peak)} $$ \text{Kurtosis} \approx 3 \implies \text{Mesokurtic (similar to normal distribution)} $$

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm, skewnorm
from scipy.stats import skew, kurtosis

# Generate data points
np.random.seed(42)  # for reproducibility
n_points = 1000

# Normal distribution
normal_data = np.random.normal(loc=0, scale=1, size=n_points)
skewness_normal = 0

# Right-skewed distribution (using a different distribution for better visual)
right_skewed_data = np.random.exponential(scale=1, size=n_points) - 1 # Shifted exponential
skewness_right = skew(right_skewed_data)

# Left-skewed distribution (mirroring the right-skewed)
left_skewed_data = - (np.random.exponential(scale=1, size=n_points) - 1)
skewness_left = skew(left_skewed_data)

# Plotting histograms
plt.figure(figsize=(14, 6))

plt.subplot(1, 3, 1)
plt.hist(normal_data, bins=30, density=True, alpha=0.7, color='blue', label='Normal')
xmin, xmax = plt.xlim()
x_norm = np.linspace(xmin, xmax, 100)
p_norm = norm.pdf(x_norm, np.mean(normal_data), np.std(normal_data))
plt.plot(x_norm, p_norm, 'k', linewidth=2)
plt.title(f'Normal (Skewness ≈ {skewness_normal:.2f})')
plt.xlabel('Data Value')
plt.ylabel('Probability Density')
plt.legend()

plt.subplot(1, 3, 2)
plt.hist(right_skewed_data, bins=30, density=True, alpha=0.7, color='green', label='Right-Skewed')
xmin_right, xmax_right = plt.xlim()
x_right = np.linspace(xmin_right, xmax_right, 100)
p_right = skewnorm.pdf(x_right, a=skewness_right, loc=np.mean(right_skewed_data), scale=np.std(right_skewed_data)) # Using skewnorm to fit
# Note: Fitting skewnorm might not perfectly match the exponential, but shows the skewed shape
plt.plot(x_right, p_right, 'k', linewidth=2)
plt.title(f'Right-Skewed (Skewness ≈ {skewness_right:.2f})')
plt.xlabel('Data Value')
plt.ylabel('Probability Density')
plt.legend()

plt.subplot(1, 3, 3)
plt.hist(left_skewed_data, bins=30, density=True, alpha=0.7, color='red', label='Left-Skewed')
xmin_left, xmax_left = plt.xlim()
x_left = np.linspace(xmin_left, xmax_left, 100)
p_left = skewnorm.pdf(x_left, a=skewness_left, loc=np.mean(left_skewed_data), scale=np.std(left_skewed_data)) # Using skewnorm to fit
# Note: Fitting skewnorm might not perfectly match the mirrored exponential, but shows the skewed shape
plt.plot(x_left, p_left, 'k', linewidth=2)
plt.title(f'Left-Skewed (Skewness ≈ {skewness_left:.2f})')
plt.xlabel('Data Value')
plt.ylabel('Probability Density')
plt.legend()

plt.tight_layout()
plt.show()

_images/496f4871e605c087f32493b06b147b14cbb25288fed12c3ad3b3b0e8e3ca2580.png

# Your code here

🔍 Detecting and Handling Missing Data in Pandas#

Reindexing#

Reindexing allows you to change/add/delete the index on a specified axis:

import numpy as np
import pandas as pd

# Create sample data
dates = pd.date_range("20130101", periods=6)
df = pd.DataFrame(np.random.randn(6, 4), index=dates, columns=list("ABCD"))

# Reindex with additional column
df1 = df.reindex(index=dates[0:4], columns=list(df.columns) + ["E"])
df1.loc[dates[0] : dates[1], "E"] = 1
print("DataFrame with missing data:")
df1

Dropping Missing Data#

Use .dropna() to remove rows/columns with missing values:

# Drop rows with any missing values
print("After dropping rows with missing data:")
df1.dropna(how="any")

Filling Missing Data#

Use .fillna() to fill missing values with a specified value:

print("After filling missing data with 5:")
df1.fillna(value=5)

Detecting Missing Values#

Use isna() or isnull() to get a boolean mask:

print("Boolean mask for missing values:")
pd.isna(df1)